Os blocos lógicos são mais um elemento pertencente ao material estruturado, ou seja, todo aquele que é organizado segundo critérios precisos. Podem ser confeccionados em madeira, plástico ou cartolina com diferentes tamanhos, espessura e cores.
Os blocos lógicos foram criados na década de 50 pelo matemático húngaro Zoltan Paul Dienes e são uma material estruturado de classificação que tem a capacidade de associar à dinâmica a lógica e o raciocínio abstrato.
Constituem um material extraordinário para estimular na criança, a análise, o raciocínio e o julgamento, partindo da ação, para então desenvolver a linguagem. De 1890 a 1934 foram utilizados de modo sistemático com crianças pelo psicólogo russo Vygotsky, quando ele estudava a formação dos conceitos infantis.
Fazendo referência a Piaget, ” a aprendizagem da matemática envolve o conhecimento físico e o lógico-matemático. No caso dos blocos, o conhecimento físico ocorre quando a criança pega, observa e identifica os atributos de cada peça. O lógico-matemático se dá quando ela usa esses atributos sem ter o material em mãos (raciocínio abstrato)”

Os objetivos dos blocos lógicos prendem-se em:
- Desenvolver o pensamento lógico e matemático;
- Abstração;
- Conhecimento das figuras geométricas;
- Desenvolver o conhecimento dos atributos e dos critérios de cada peça dos blocos lógicos;
- Desenvolver a imaginação e espírito crítico, dependo do contexto de jogo sugerido para a criança desenvolver;
- Material de multidisciplinaridade, dependendo da intencionalidade das propostas de atividade.
Os blocos lógicos são caracterizados por serem um material com estrutura eficiente no desenvolvimento lógico-matemática da criança. Recorrendo à classificação a criança pode desenvolver conceitos como cor (amarelo, vermelho e azul), forma (quadrado, rectangulo, triangulo e círculo), tamanho (grande, pequeno), e espessura (fino, grosso).
É composto por 48 peças de madeira ou plástico ou cartolina com diferentes tamanhos, espessuras e cores. Classificadas pelos seguintes atributos:
- cor;
- Tamanho;
- Forma;
- Espessura.
Fazem parte dos blocos lógicos as seguintes figuras geométricas:
- O triângulo;
- O quadrado;
- O retângulo;
- O círculo.
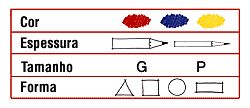
Para cada figura geométrica existem 4 atributos. Ex: a figura: quadrado, vermelha, grande e fina.
Para cada um dos atributos existe um código, da cor, da forma, da espessura e do tamanho.
Etapas dos Blocos Lógicos
É fundamental abordar os blocos lógicos de maneira gradual, e então, seguir as diferentes etapas:
- Exploração livre: manipular as peças livremente, nesta etapa o importante é apresentar todas as 48 peças às crianças;
- Proporcionar jogos onde os quatro atributos sejam desenvolvidos sequencialmente. Criar, recriar, o trabalho dos atributos de forma lúdica e através de um ordem sequencial partindo do grau de dificuldade. Deve-se inicar pela cor, quando este conceito apreendido passar para a forma, depois o tamanho e por fim a espessura.
- É necessário que estas análises terminem sempre na tabela de atributos, mesmo que só se trabalhe, um, dois ou três dos atributos.
- A terceira etapa só se deve iniciar após todas as outras estarem interiorizadas Trabalha-se as 48 peças dos blocos lógicos através de actividades com diagramas.
Tabela de Atributos
O trabalho desenvolvido fica facilitado se registado na tabela de atributos. Os atributos devem ser introduzidos gradualmente. A tabela deve ser apresentada contendo apenas os atributos que as crianças já conseguem classificar. Este também é um modo de mostrar com mais clareza, os conjuntos que são possíveis (as peças de cada coluna ou de cada fila são sempre um conjunto).
O número de filas deve ser acrescentado ou diminuído dependendo do numero de classificações que se faça. A peça classificada deve ser sempre posta no início da fila, para que a criança consiga fazer uma associação entre a classificação e a peça classificada.
Digramas de Veen, de Carrol e de Árvore
Os diagramas são representações de conjunto, de relações matemáticas e de relações lógicas.
Diagrama de Veen
Exemplos de exercícios:
- Quantos aquários são necessários formar para caberem os peixinhos triangulares, azuis, finos, grandes?
Só é necessário um aquário, por só existe 1 triângulo, azul, fino e grande.
- Coloca dentro do aquário todos os peixes triangulares, de todas as cores, finos e grossos.
Pode acontecer surgirem problemas que necessitem de fazer outro conjunto dentro do conjunto já existente. A esses chamamos de subconjuntos. Aqui utilizam-se as etiquetas.
- Forma um subconjunto dos animais triangulares vermelhos
Diagrama de Carrol
O diagrama de Carrol divide o plano em quatro regiões associando a cada uma delas dois atributos: um na direcção vertical e outro na direcção horizontal. Então, para se conseguir posicionar uma peça no jogo a criança tem que ter em conta dois critérios de classificação ao mesmo tempo.
Este pode ser um ponto interessante para introduzir a negação do atributo; “vermelho” - “não vermelho”
Diagrama de Árvore
É possível criar para este jogo 4 diagramas de árvore, cada um correspondendo a um atributo: cor, forma, tamanho e espessura.
É um jogo que tem de ser desenhado previamente pela educadora e deve ser apresentado em tamanho real às crianças.
Este diagrama consiste num tronco que se subdivide em tantos ramos quantos forem os valores de cada atributo. Desta forma a cada galho da árvore vão sendo associados os critérios de classificação das peças do jogo.
Da espessura:
Do tamanho:
Da cor:
Da forma:
Retirado do site: http://4pilares.zi-yu.com/ 








Nenhum comentário:
Postar um comentário